В первой из 63-х частей серии, исследующей мир субтрактивного синтеза (subtractive synthesis), Гордон Рид объясняет читателю основы физики звука. Что такое звуковая волна (Waveform) и гармоники (Harmonics), откуда они берутся и как теория связана с практикой?

Далее, перевод текста статьи. В скобках указаны термины на языке оригинала.

Я рассмотрю основные принципы наиболее распространенной формы звукового синтеза — субтрактивного синтеза (принципы хорошо известные), а затем в последующих частях серии — как эти принципы применяются на конкретных синтезаторах, звуковом дизайне и музыке в целом. Если у вас есть синтезатор, который работает на основе субтрактивных принципов, и вы знаете, как получить из него звуки, которые вам нравятся, но не понимаете, почему или как получаются эти звуки, эта серия заполнит некоторые теоретические пробелы. Теперь: что такое субтрактивный синтез?

Название «субтрактивный синтез» происходит от самого метода, в котором вы ослабляете (делаете заметно тише) или удаляете гармонии из гармонически насыщенных сигналов для создания новых звуков. Это можно делать статично, чтобы создавать простые тоны, или использовать средства, предлагаемые фильтрами (filters), генераторами огибающей (envelope generators) и модуляторами (modulators) в вашем синтезаторе или программном обеспечении для создания динамических звуков, которые изменяются относительно времени своего звучания. Но… Возможно, я уже вас запутал. Что такое гармоники? Что за звуковые волны? Откуда они берутся в природе? В этой статье я отвечу на эти три вопроса.

Во всем виноваты греки

Чтобы ответить на такие фундаментальные вопросы, мы должны запрыгнуть в нашу машину времени и отправиться в темные недра истории человечества. Задолго до искусственного моделирования звуков, до сэмплеров, до аналоговых полифонических синтезаторов, даже до появления клавишных инструментов…

Тут мы нагло врываемся на территорию Доктора Кто, потому что нам нужно вернуться аж на 2500 лет назад и познакомиться с парнем из Ионии по имени Пифагор. Пифагор был, пожалуй, первым в мире профессиональным математиком, но мы относительно мало знаем о нем и его достижениях (большая часть того, что мы знаем не более чем легенды: то, что каждый школьник воспринимает как теорему Пифагора — задолго до его рождения уже было известно в Вавилоне) Но речь не об этом.

Одним из менее известных открытий, приписываемых Пифагору, было то, что две одинаково натянутые струны дают приятный уху звук при щипке, если их длины соотносятся с простыми числами (то есть целыми числами) Простыми словами: Пифагор открыл законы музыкальной гармонии.

Легенда гласит, что учитель однажды прогуливался и услышал звуки молотов из кузницы, которые ковали железо; прислушавшись к ним, он понял, что их стук создает гармонию. Позже, опытным путем Пифагор установил, что различие звуков зависит только от массы молотка, а не от других характеристик. Потом философ сделал из струн устройство с различным количеством гирек; струны крепились к гвоздю, который был вбит в стену его дома. Ударяя по струнам, он вывел понятие октавы, и то, что её соотношение равно 2:1, открыл квинту и кварту. Затем Пифагор сделал устройство с параллельными струнами, которые натягивались колками. С помощью этого инструмента он установил, что определенные созвучия и законы есть во многих инструментах: флейтах, цимбалах, лирах и других устройствах, с помощью которых можно производить ритм и мелодию.

Например, если одна струна в два раза длиннее другой (в соотношении 1:2), звучало довольно красиво. Соотношение 2: 3 — тоже приятно ласкает ухо.

Пифагор был настолько поражен своим открытием, что возвел цифры в культ. Нумерология станет основой его философии. Музыкальная гармония в учении Пифагора является моделью вселенской гармонии, которая состоит из нот — различных аспектов Мироздания. К сожалению, он и его последователи затем немного слетели с катушек, пытаясь определить аналогичные числовые соотношения для астрономических явлений и орбит пяти известных в то время планет планет, солнца и луны, что породило мифическую «музыку сфер».

Но почему струны у Пифагора имеют целочисленные отношения? Почему приятный уху звук не возникает, если, например, одна из струн в 1,21346706544 раза длиннее другой?

Давайте дернем струну

Чтобы начать отвечать на этот вопрос, взгляните на натянутую струну: она зафиксирована на обоих концах, но свободно вибрирует по всей своей длине.

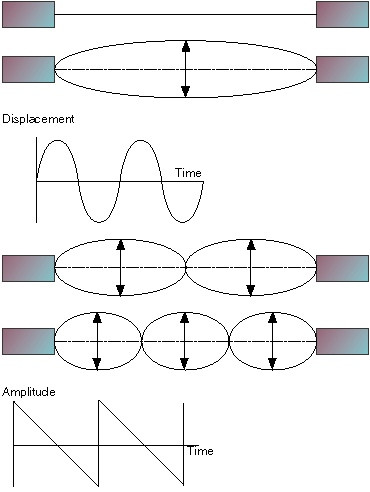
(На рисунке 1 показана такая строка в состоянии покоя)

Теперь представьте, что мы аккуратно щипаем струну ровно посередине. Как вы уже догадались: это заставляет её вибрировать так, как показано на рисунке 2.

Это пример «стоячей волны» (Standing wave). Если вибрация (или «колебание» (oscillation)) так же проста, как показано на рисунке 2, точка в центре струны перемещается по простой повторяющейся схеме, называемой синусоидальной волной (см. Рисунок 3). Такое колебание принято называть звуковой волной (waveform), а частота, с которой звуковая волна завершает один «цикл» за одну секунду, называется «фундаментальной» частотой струны.

Фундаментальная частота не единственное состояние вибрации струны — хотя из–за того, что она зафиксирована на обоих концах, количество вибраций строго ограничено её длинной. Представьте себе, что вы помещаете палец на центр струны, щипая ее по обе стороны от пальца (так, чтобы струна все еще вибрировала по всей своей длине). На рисунке 4 видно, что вибрация в половину длины оригинальной волны возможна. Точно так же будет если вы отсчитаете пальцем одну треть длины струны (рисунок 5) и так далее.

Такие волны (standing waves) возможны во всех целочисленных соотношениях, показанных на рисунке 2. Их и называют «гармониками» основной частоты.

Если серьезно озаботиться математикой стоячих волн, обнаружим, что такую волну можно представить как две «бегущие» волны, движущиеся вдоль струны в противоположных направлениях (нет, не спрашивайте почему, или мы будем здесь вечно). Знание этого, однако, приводит нас к простому выводу: если вы уменьшите длину волны пополам, частота требуемых «бегущих» волн удвоится. Точно так же, если вы разделите длину волны в три раза, вы утроите частоту; четверть длины волны — и вы умножаете частоту на четыре, и так далее…

Так или иначе, мы теперь ответили на наш первый вопрос: что такое гармоники — это меньшие вибрации «поверх» друг друга в целочисленных соотношениях к фундаментальной частоте, которые возникают в процессе колебания струны. Конечно, этот анализ относится не только к вибрирующей струне. Например, воздух в комнате. На мгновение, забывая о любых мелочах, таких как, мебель, воздух может вибрировать в любом месте комнаты кроме стен, пола и потолка. Другими словами, вибрации воздуха в комнате ограничены так же, как вибрации струны (своими нулевыми отметками). Вот почему обычные комнаты имеют «резонансы» — они являются гармоническими частотами самой комнаты. И именно поэтому органы в соборах имеют характерный звук: их трубы — это тоже простые гармонические осцилляторы.

Во всех случаях, кроме некоторых эзотерических, первая гармоника (фундаментальная, называемая f) — это тон, который вы определяете, когда слушаете звук. Вторая гармоника (также называемая первый «обертон») составляет половину длины волны основной частоты и, следовательно, в два раза больше по своей частоте. В изоляции мы воспринимаем это как тон , который на одну октаву выше основного.

Третья гармоника имеет частоту 3f (которая является чистой квинтой, на полторы октавы выше основного тона), а четвертая гармоника с частотой 4f определяет вторую октаву. Следующие три гармоники лежат в следующей октаве, а восьмая гармоника определяет третью октаву выше основного тона. И так далее.

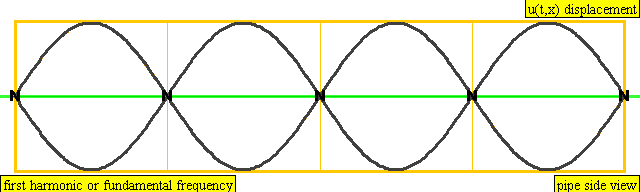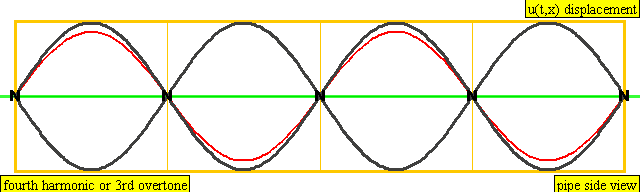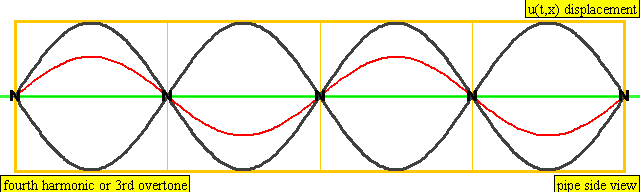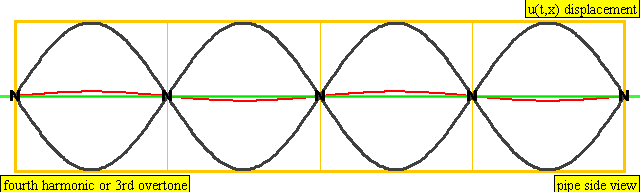
Это та информация, которая нам необходима для понимания наблюдения Пифагора. В соотношении 1:2 короткая струна имеет фундаментальную частоту равную второй гармонике длинной струны. Это ровно на октаву выше. В примере струн в соотношении 2:3 третья гармоника длинной струны имеет ту же частоту, что и вторая гармоника короткой. Другими словами, гармонические структуры двух струн тесно связаны друг с другом, и мы воспринимаем такой звук, как музыкально «приятный».

Природа звука

Теперь разберем: когда вы дергаете струну, вы не слышите звук лишь одной гармоники. Условия для создания такого чистого тона — в реальном мире — почти невозможны, поэтому любой естественный тон, вероятно, будет состоять из множества гармоник, присутствующих в разных количествах. В любой момент именно их комбинация определяет форму волны звука, и из–за количества присутствующих гармоник звуковая волна будет гораздо сложнее, чем простая синусоида, показанную на рисунке 3 (выше). Вам нужно только взглянуть на образец звука гитары или человеческого голоса в аудиоредакторе, чтобы увидеть, насколько сложной может быть реальная звуковая волна.

Синтез звука был бы невозможным, если бы не французский математик Жан Батист Жозеф Фурье. Парень с яркой жизнью, Фурье был учителем, тайным полицейским, политзаключенным, губернатором Египта, префектом и другом Наполеона. Несмотря на это, он все же нашел время, чтобы определить, что любое периодическое движение, независимо от того, насколько оно сложное, можно разбить на его гармонические составляющие. Эта процедура называется анализом Фурье. Кроме того, анализ Фурье также показывает, что при наличии набора гармоник вы можете получить уникальный звук.

Подожди секунду… Звуковые волны определяют гармоники, а гармоники определяют звуковые волны? Очевидно, что гармоники и формы волны — это всего лишь два способа выразить одно и то же. Это ключевой момент: природа музыкальных тонов определяется количеством и амплитудой гармоник, содержащихся в них, и любой данный набор гармоник дает нам заданную форму волны. Поэтому, когда мы смотрим на генераторы на синтезаторе и видим такие вещи, как «квадратные» волны или «пилообразные» волны, это просто сокращенный способ сказать: «Этот параметр генерирует определенный набор гармоник с амплитудами x, y и z…»

Субтрактивный Синтез

Итак, давайте применим эти идеи к синтезатору. Посмотрите на форму волны на рисунке 6 (выше). Вы найдете ее почти на каждом синтезаторе, когда-либо созданном. Это идеальная пилообразная волна, названная так из–за своей формы.

Такая звуковая волна имеет простые гармонические отношения, выраженные следующим образом:

Каждая гармоника присутствует, а амплитуда n-й гармоники в 1 / n раз больше основной.

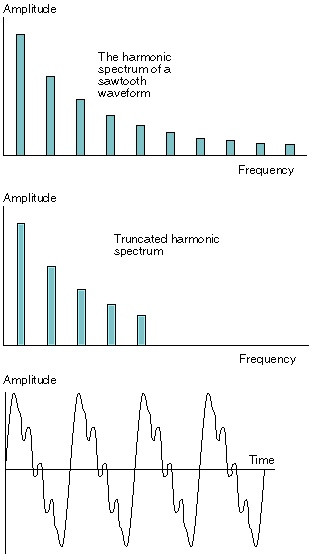
на рисунке 7 показаны первые 10 гармоник в пилообразной волне. Можно увидеть, как они уменьшаются на более высоких частотах.

Но что произойдет, если вы удалите эту серию гармоник? Допустим, вы удалили все кроме первых пяти из них (для которых вам нужно устройство, называемое «фильтром»). На рисунке 8 показан этот спектр, а на рисунке 9 показана форма волны, которой он соответствует.

Как видите, новая форма волны отличается от пилообразной волны. Она звучит по-другому. Различие между ними состоит в том, что вы обрезали гармонический ряд пилообразного зуба так, чтобы осталась только первая горстка гармоник. Другими словами, вы использовали «фильтр» для «вычитания» гармоник, создавая новую форму волны и, следовательно, новый звук.

Добро пожаловать в мир субтрактивного синтеза!

Переведено для проекта «Бык на крыше»

Оригинал статьи