Беседы с Жаком Лаканом. Интервью Жан-Пьера Пети. Часть 2
Интервью, которое физик Жан-Пьер Пети дал клиническому психологу Фабрису Гийо, о его первой встрече с Жаком Лаканом летом 1979 года, посвященное поверхности кросс-кап и топологическим разработками французского психоаналитика.
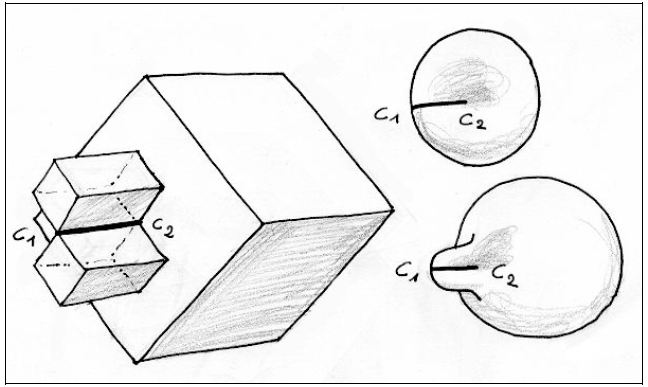
Жан-Пьер Пети: Вторая встреча, которая состоялась через несколько недель после первой погрузила Лакана в бездну недоумения. Я подготовил целую серию рисунков, достаточно ясных, чтобы объяснить ему, как я представлял способ перемещения двух точек Пинча на
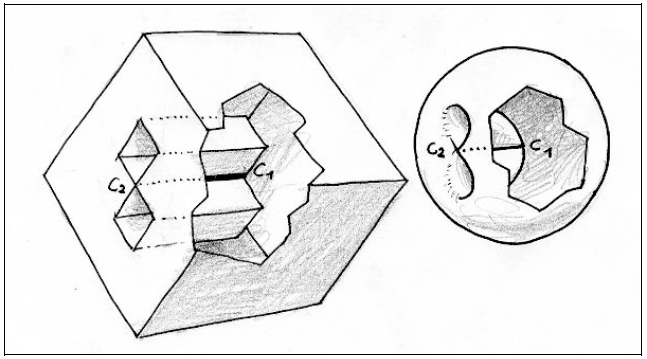
Это будет небольшая интермедия на тему «Для чего может служить процедура выворачивания сферы? ". Здесь: для того, чтобы поменять местами две точки Пинча на
Все, что мы знаем, это что в конце операции у нас будет два вида инвагинаций, которые увидел бы наблюдатель, находящийся «внутри» первоначального кросс-капа (это неподходящее выражение, поскольку это односторонняя поверхность).
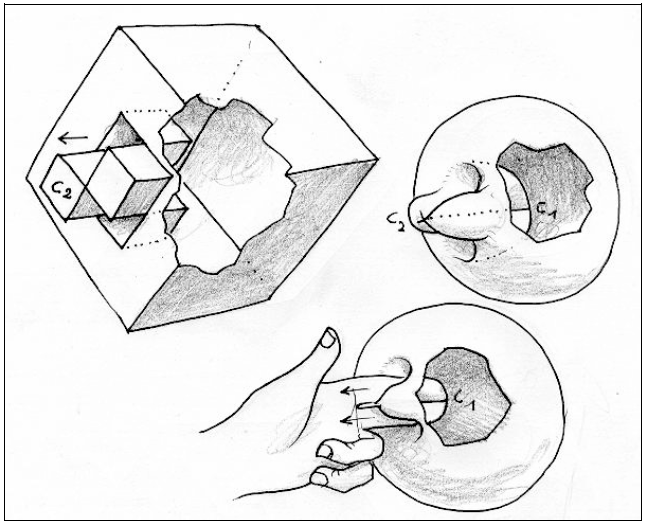
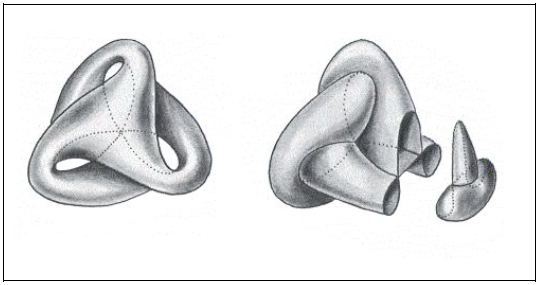
Полиэдрическая репрезентация чертовски удобна, чтобы не терять нить этих операций. Все, что остается, это ввести два пальца в эти инвагинации и вытянуть все наружу (рис. 6).
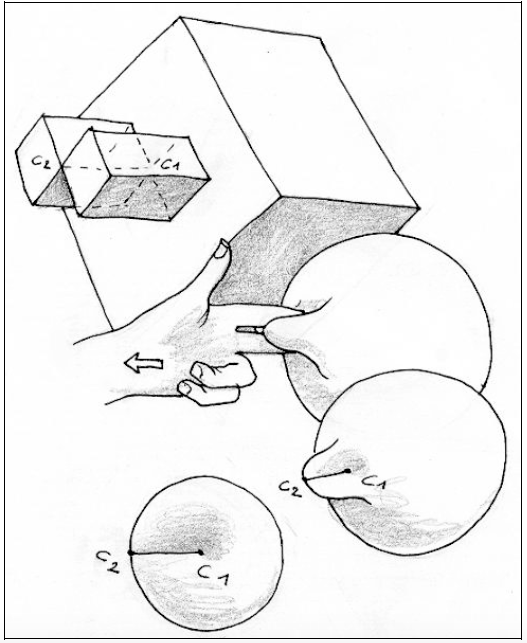
Остается только завершить эту операцию (рис. 7).
Представляется, что Лакану потребовалось бы немало времени, несколько часов,чтобы он признал законность этого геометрического «фокуса». Но в этот раз Лакан так организовал свое время, что в нашем распоряжении была вся вторая половина дня.
Дело было совершенно ясно. Поверхность, называемая кросс-капом, имела две эквивалентные точки Пинча, поскольку их можно менять местами, приводя ту, что в «центре», к «периферии», и наоборот. У меня было впечатление, что я создал приличный беспорядок в геометрических концепциях Лакана.
Прежде чем пережить этот опыт, я ничего не знал о личности Лакана, его статусе «гуру». Я бы сказал, что чувствовал себя как доставщик пылесоса , которому клиент задает вопросы по поводу его использования. Он лишь подчеркивал мои замечания ремарками. Думаю, я мог бы восстановить отрывки диалога.
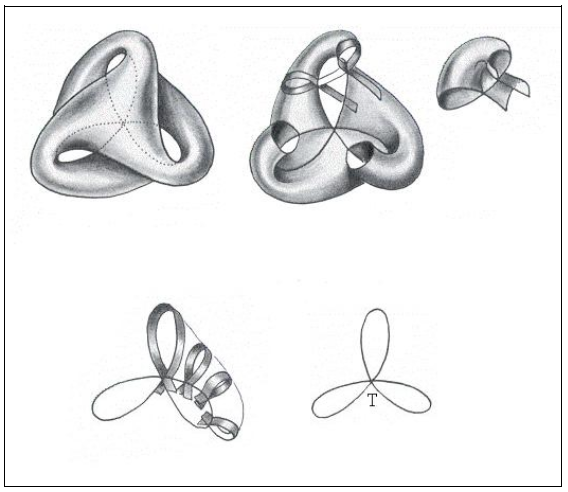
— Так, на поверхности Боя (рис. 8), нет точек Пинча?
— Нет.
— Но что это за точка в центре?
Это тройная точка Т (рис. 9), место тройного самопересечения поверхности. Но она не существует геометрических «интринсек»*-свойств
— Что вы хотите этим сказать?
— Что это «обстоятельство» связано с репрезентацией в нашем трехмерном пространстве, так же, как и линия самопересечения бутылки Клейна тоже связана со способом репрезентации.
— Тогда мы можем действовать так, как будто ее не существует.
— Точно. С другой стороны, если вы решили сделать сетку на поверхности, образовав ее с помощью двух видов кривых, тогда появляется один полюс (рис. 10), который существует интринсек, так же, как, когда вы делаете сферу с системой меридианов и параллелей, у вас будет два полюса. Эти полюсы неустранимы. Тогда как в торе или бутылке Клейна можно избежать появления этих полюсов.
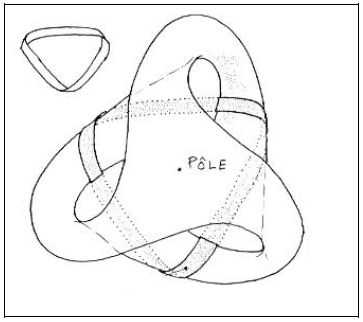
У меня было отчетливое впечатление, что Лакан нашел новую «игрушку», и что кросс-кап внезапно перестал его интересовать. По крайней мере мне так казалось до конца этой встречи. Он искал одностороннюю поверхность, у которой была бы только одна сингулярная точка. Ответ казался очевидным: это поверхность Боя. Он внимательно смотрел на мои рисунки.
— Как разрезать эту поверхность?
— Вы хотите сказать «как вписать кривую вокруг полюса»?
— Да, вокруг него. Именно так.
— Это просто. Очевидно, немного сложно понять, каким образом кривая вписывается на эту поверхность. Её окрестность напоминает лейбл марки прачечной “Woolmark”(рис. 11), это лента Мебиуса с тремя полуоборотами.

— Замечательно!
— Будет проще, если я смогу принести вам трехмерную модель из картона.
— Вы могли бы это сделать?
— Нет проблем.
— Если бы вы это сделали, то доставили бы мне огромное удовольствие.
— Это просто. Совсем скоро я планирую повидаться с моим другом математиком Андре Лихнеровичем, который также заинтересован во всем этом. Я планировал построить три модели: кросс-капа, центральную модель с четырьмя ушками, открытую Мораном, и модель поверхности Боя. После того как я покажу их ему, я оставлю ему центральную модель, а вам принесу модель поверхности Боя.
— Буду ждать с нетерпением.
*интринсек — (внутреннеприсущие) свойства топологического объекта.
Перевод — Алексей Зайчиков
Перевод сделан для группы Lacan et autour de lui
